有效扩散是评价多孔介质输运的重要宏观性质。对分割的三维CT图像进行数值计算,可以精确估计扩散特性。另一方面,孔隙空间的几何描述符,如孔隙率、比表面积和其他与输运相关的描述符,可以很容易地从3D CT图像中计算出来,并且与扩散过程密切相关。然而,对这些描述符与各种多孔结构的扩散特性之间的定量关系的研究仍在进行中。在本文中,我们考虑了每种壤土和砂土的三种不同的土壤样品,共六个样品,使用几何孔隙空间描述符的单变量和二元概率分布对其三维微观结构进行了定量研究。这些信息用于通过经验推导的回归公式来研究微观结构-性质关系,其中特别关注壤土和砂样品之间的差异。由于这些公式的分析性质,可以更深入地了解三维孔隙空间形态与由此产生的扩散特性之间的关系。特别是,研究表明,目前文献中用于预测土壤气体扩散的公式可以通过纳入进一步的几何描述符(如测地线扭曲度、弦长或孔隙空间的收缩性)来显着改进。通过拟合不同数据集上的回归参数以及将经验推导的回归公式应用于不用于模型拟合的数据,研究了这些公式的稳健性。其中,基于孔隙度以及测地线扭曲度的平均值和标准差的公式在确定系数和平均绝对百分比误差方面表现最好。此外,对于扩散特性的预测,测地线扭曲度的概念优于几何扭曲度,后者是基于孔隙空间骨架的形成。
孔隙空间的三维形态对多孔介质的有效宏观性质有很强的影响Sahimi (2011);熊(2018);冲(2017)。其中,从锂离子电池到固体氧化物燃料电池,再到土木工程Bear(2018),扩散特性在广泛的应用中都引起了极大的兴趣;纽曼和托马斯-阿利亚(2004);Cooper et al. (2013);Das et al. (2018);冲(2017)。同样,孔隙空间的三维微观结构也极大地影响了土壤中的水、气和碳通量(Rabot et al., 2018)。土壤结构介导的气体输送的一个典型例子是温室气体排放到大气中,Smith等人(2003)。众所周知,土壤中的气体输送主要是一个以扩散为主的过程。更准确地说,气体在土壤中的扩散主要是由所谓的土壤气体扩散率控制的,对于这种经验关系,即回归公式(也称为分析预测公式),已经利用容易获得的土壤体积特性,如充气孔隙度Millington (1959);笔者(1940);Marshall(1959),然后通过整合其他土壤特性如土壤容重,Millington和Quirk(1961)进一步改进;Moldrup等人(2000);Deepagoda等人(2011)或比表面积Moldrup等人(2001)。此外,事实证明,可以通过纳入孔隙空间的进一步几何描述符来改进这种类型的回归公式Prifling等(2021)。这促使人们对孔隙空间进行更详细的表征。
由于近年来在土壤成像领域的努力和技术进步,特别是在x射线计算机断层扫描(CT),它可以准确地可视化和表征土壤孔隙空间的三维高分辨率。因此,x射线CT也提供了前所未有的机会来测试孔隙空间物理描述符在预测土壤气体扩散率的经验关系中的有效性和相关性。以往依靠x射线CT获得气体输运参数的研究迄今为止都取得了令人满意的结果。在对亚热带气候下的免耕系统的研究中,发现x射线CT得出的孔隙度与相对气体扩散率和透气性的对数之间存在显著相关性。da Silva et al.(2021)。在Katuwal et al.(2015)的另一项研究中,通过x射线CT获得的孔隙度也被证明与透气性有很好的相关性。此外,在Katuwal等人(2015)中,研究表明,从标准气体测量(如Buckingham(1904)所述)获得的集总扭曲度-连通性参数与从x射线CT获得的参数之间存在很强的相关性。因此,根据文献,x射线CT似乎可以被认为是一个强大的工具,以获得气体输运参数。然而,目前还不清楚哪种几何描述符组合可以用来最好地预测有效的宏观性质作为有效扩散率。
同样,计算能力的进步和复杂的数值方法使得从声音数学理论Ray et al.(2018)中计算与方向相关的扩散特性成为可能。这是可能的,甚至在一个广泛的真实的数据集,因此相当复杂的几何形状,这形成了基础的定量调查微观结构-性质的关系在本研究中。我们特别考虑了三维微观结构描述符与扩散特性之间的关系。
在本文中,我们考虑了不同类型的回归公式来预测三维孔隙空间的几何描述符的扩散特性。将这种方法应用于两种不同土壤质地的数据,我们定量地研究了所考虑的回归公式的性能和鲁棒性。我们深入研究了样品孔隙空间三维微观结构的几何描述符,并在砂和壤土的背景下对其进行了详细分析。为此,所考虑的壤土和砂土样品以及相应的层析成像技术分别在2.1节和2.2节中进行了说明。此外,我们还详细介绍了扩散特性的数值计算(第2.3节)以及三维孔隙空间形态的各种描述符(第2.4节),这些描述符用于几何上表征其三维微观结构和扩散特性。最后,在第2.5节中,我们说明了模型拟合和验证的方法,这些方法用于评估微观结构-性能关系的预测能力。然后,在3.1节中,对4608个子样本进行统计分析,通过单变量和双变量概率分布来定量研究壤土和砂土之间的差异。此外,在3.2节中建立了土壤气体扩散的微观结构-性质关系,其目标是推导出准确的(可能是通用的)预测公式,即,它们不需要为两种土壤质地单独设置拟合参数。与其他数据科学方法(例如神经网络)相比,经验推导的预测公式在孔隙空间的三维形态与其扩散特性之间建立了可解释的关系。特别是,在第4节中,我们比较了文献中讨论的常规模型与更复杂的模型的预测能力,这些模型还包括三维孔隙空间形态的进一步几何描述符。事实证明,通过这种方式获得的更精确的微观结构描述使我们在决定系数和平均绝对百分比误差方面超越了传统的预测公式。此外,定量比较了两种不同的扭曲度概念,即测地线扭曲度和几何扭曲度,以研究它们在建立微观结构-性能关系方面的适用性。第5部分总结了本文并概述了未来研究的可能性。
本研究分析的样本是在Lippold et al.(2021)中描述的植物生长实验框架内获得的。特别是,高度和直径的圆柱形柱被土壤包裹,其中使用了两种不同的基质(壤土和沙子)。壤土基质从单片Phaeozem土壤剖面的上部获得,干燥至10%的重量含水量,然后筛选到。砂岩基质由83.3%的石英砂(wf33, Quarzwerke Weferlingen,德国)和16.7%的筛分壤土组成。有关这些基质的化学和物理性质的详细信息请参见Vetterlein等人(2021)。壤土罐填充均匀,容重为;砂土罐填充容重为。生长结束时,从5、10和深度(每个基板3个,每个深度1个)共取6个样品(高度和直径的铝环),存放在密封塑料袋中,然后进行x射线CT扫描。
x射线CT扫描采用工业CT扫描仪(X-TEK XTH 225,尼康计量),包括Elmer-Perkin 1620探测器面板(px)。扫描仪的工作电流为。在样品的完整旋转过程中,总共获得了2748个投影,每个投影的曝光时间为1。利用CT Pro 3D软件(Nikon Metrology) Banhart(2008),通过滤波后的反投影算法,将得到的图像重构为三维层析图。在重建过程中,灰度范围用百分位拉伸法进行归一化,该方法将0.2%的最暗和最亮体素分别设置为0和255,并在两者之间进行线性拉伸。体素大小等于。
使用二维非局部均值滤波器()和非锐利掩膜滤波器(半径=1,权值=0.6)对灰度图像进行去噪和对比度增强。Buades等(2005);Burger和Burge(2016)。随后对图像进行二值化,以区分孔隙空间和土壤基质。为了充分客观地选择全局阈值,采用了Otsu(1979)提出的自动阈值检测方法。
对于每个纹理和深度,样本被截断为每个体素的1536个切片的堆栈。这与长方体的高、宽、长一致。为了研究的目的,我们进一步将长方体划分为不重叠的立方体切面,每个切面以体素()表示。因此,我们为每个深度和土壤质地获得了768个立方切割,这导致总共有4608个子样本。所选子样本如图1所示。
最后,去除孤立的孔隙,孔隙度变化很小,即三维二值图像中没有连通的孔隙很少。壤土孔隙度的总体差异小于初始孔隙度的2%,砂土甚至小于0.5%。

选定的壤土(上一行)和砂(下一行)子样本的三维效果图,其中固相以灰色表示。这三列分别对应最小(左,)、平均(中,)和最大(右,)孔隙度
具有浓度场的化学物质在多孔介质中的扩散输运,其最简单形式可以用拉普拉斯方程来描述
(1)式中为有效扩散张量,是输运模型的基本输入。它包含了所考虑的多孔介质特有的所有信息。然而,对(天然)多孔介质进行表征是相当困难的。如果底层几何是可用的,例如,从二进制CT数据中,确定张量的一种可能性是应用均匀化理论(Hornung, 1997)的结果;Ray等人(2018),最初是为周期性设置导出的。
为了在合理的时间范围内对均匀化的有效扩散系数进行数值模拟,将8个体素合并为1个(超)体素,对子样本进行粗化处理。如果4个原始体素为实体体素,4个为虚体素,则生成的(超)体素随机转换为虚体素或实体体素,否则大多数定义生成体素的类型。因此,执行此过程后,子样本的维度为体素(),其中体素对应于。
对于连通的、足够光滑的孔空间和互补的固相,扩散张量的项为
(2)具有分子扩散性和以下补充细胞问题,
(3)其中,V(Y)表示V的体积,是固体相的单位外法线,是j方向的单位矢量,是克罗内克函数。注意,在目前的设定中,我们假设固相内的扩散系数为零。
(3)中给出的偏微分方程在连通孔隙空间内求解,并使用局部不连续伽辽金(LDG)方法进行离散化(Aizinger et al. (2018);Rupp and Knabner(2017),这是在并行有限元软件m++ wiener(2005)中实现的。通过Trilinos Heroux和Willenbring(2003),使用BiCGstab求解器和ILUT前置条件Saad(2003)的组合来求解所得到的线性系统。
如上所述的计算结果,已经确定了从砂和壤土的x射线CT扫描中获得的所有4608个子样本的扩散张量,如第2.2节所述。关于这些扩散张量分析的进一步细节,请参见Prechtel等人(2022)。下面,沙土和壤土亚样的土壤气体扩散将用有效扩散系数和本然扩散系数的比值来描述,该系数有时被称为微观结构因子或m因子Gaiselmann等人(2014)。特别地,我们在三个笛卡尔轴方向上取平均值,使得从扩散张量的对角线项中获得平均m因子为。Prechtel等人(2022)认为,土壤和砂土样品均未表现出明显的各向异性效应。
在本节中,介绍了三维孔隙空间形态的各种几何描述符以及从体素化图像数据中估计它们的方法。在图2中,说明了这些描述符的二维版本。
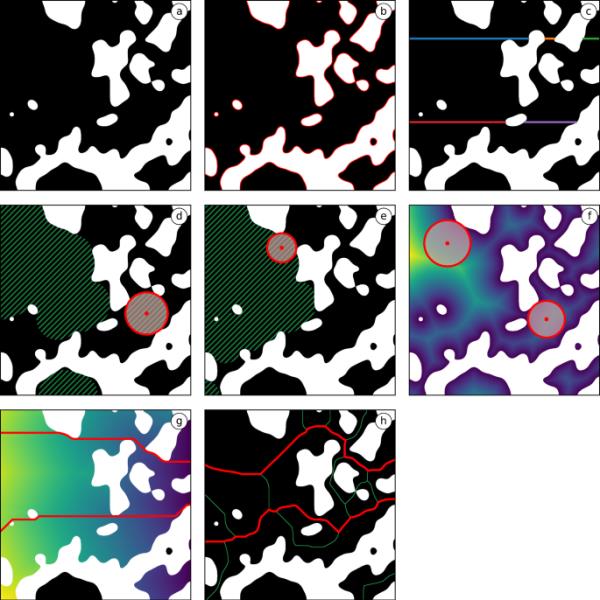
微观结构描述符的二维示意图:示例选择二维切片,其中孔隙空间用黑色表示(a);孔隙与固相之间的表面,在二维切片中表现为一维物体(b);在水平方向的和弦为两个范例选择的垂直高度水平(c);(d)和(e)定义中分别使用的孔隙空间子集;孔隙空间到土壤的最短距离(f);两条典型选择的最短路径(从左到右)(g);孔空间骨架和沿骨架的最短路径(从左至右)分别用绿色和红色表示(h)。
孔隙度是三维孔隙空间形态最基本的描述因子之一。从二值化的三维图像数据中对该几何描述符的估计是直接的,通过计算分配给孔隙空间的体素数(图2a中用黑色表示)除以整个采样窗口的总体素数来执行。
除了孔隙率外,我们还考虑孔隙空间的比表面积,用s表示。它被定义为孔隙空间与固相之间的表面积除以采样窗口的体积。然后使用Schladitz等人(2007)提出的方法从体素化的3D图像数据中估计该数量,该方法基于带有核的图像卷积,避免了实际表面的重建。在图2b中,孔相与固相的界面用红色表示。
三维孔隙空间形态的进一步描述是其弦长分布(Matheron (1975);Serra(1982),其中和弦是完全包含在预定义相位中的线段,如果不与互补相位相交,则不能进一步扩展。显然,一般来说,弦长的概率分布取决于线段的方向。我们计算了三个直角轴方向上孔隙空间的弦长分布。特别是,对于这三个方向中的每一个,我们计算相应弦长分布的平均值。在下文中,用这三个平均值的平均值表示三维孔隙空间形态。在图2c中,五个不同的和弦在水平方向上显示,并以五种不同的颜色描绘,用于两个示例选择的垂直高度水平。
为了解释这一描述符,我们首先回顾了连续孔径分布()和模拟压汞孔隙测量()的概念。连续孔径分布是一个函数,其值由孔隙空间的体积分数给出,该孔隙空间可以被(可能重叠的)具有半径的球体覆盖(使得球体完全包含在孔隙空间中)Serra (1982);Soille(2013)。此外,用最大半径表示孔隙度。请注意,图2d中绿色阴影区域对应于孔隙空间的一部分,该部分可以被具有与图2d中红色圆圈相同半径的潜在重叠球体所覆盖。
的概念与的概念相似,唯一的区别是现在由孔隙空间的体积分数给出,孔隙空间可以被半径为r的球体覆盖(可能重叠),形成从预定义方向的侵入,见图2e从左到右的球体侵入。类似地,用最大半径表示为。一般来说,取决于入侵的方向。然而,如上所述,壤土和砂土样品中缺乏明显的各向异性效应促使我们进行如下的平均。首先,分别计算三个轴向中的每一个,然后使用得到的三个值的平均值。
孔隙空间的收缩度定义为。它是衡量瓶颈效应强度的一种方法,最初由m
在这里,我们考虑从孔空间内随机选择的点到固相的最短(接触)距离的分布。它是通过Mayer(2004)提出的一种算法从体素化图像数据中估计出来的,该算法基于欧几里得距离变换Soille(2013)的计算;Maurer et al.(2003)。该分布的均值将在下文中表示为。在图2f中,孔空间中点到固相的最短距离用(较亮和较暗)颜色表示,其中亮度的增加对应于接触距离的增加。特别是,图2f中红色球体的半径对应于它们的中点到土壤的最短距离。
另一个与输运相关的量是所谓的孔隙空间测地线扭曲度。它描述了完全包含在孔隙空间中的输送路径的长度和缠绕度。从3D图像数据中,通过计算从预定义的起始平面上随机选择的孔隙体素到平行目标平面的最短路径长度,除以这两个平面之间的距离来确定(局部)测地曲率的分布,其中最短路径使用Dijkstra的Jungnickel(2008)算法计算。在图2g中,两条示例选择的最短路径(从左到右)以红色表示,其中每个孔空间像素的颜色对应到目标平面的最短距离的程度,亮度的增加对应路径长度的增加。通常,起始面和目标面选择与相关传输方向正交。对于本文考虑的图像数据,我们计算了相对于三个笛卡尔轴方向的测地线扭曲度的分布。测地线平均弯曲度由所有最短路径长度除以起始平面和目标平面之间的距离的平均值确定。类似地,标准差是这些归一化路径长度的经验标准差。
请注意,在许多应用中,仅考虑为了表征多孔介质的微观结构,尽管事实上包含有关孔隙空间的三维形态的进一步有用信息,参见3.2节进行详细讨论。此外,除了测地线扭曲,文献中还存在其他几个扭曲概念,例如Holzer等人(2022);Ghanbarian et al.(2013)进行了全面的概述。这种另类扭曲概念的一个例子是所谓的几何扭曲,这将在下一段中描述。
与上述测地线扭曲度相反,几何扭曲度(有时称为骨架化扭曲度)的概念是基于孔隙空间骨架的计算,如图2h所示,其中骨架以绿色表示。在本研究中,我们采用Lee疏化方法计算孔隙空间骨架,Lee et al. (1994);萨哈等人(2016)。与测地曲率的概念类似,沿传输方向的最短路径由Dijkstra的Jungnickel(2008)算法计算,在几何曲率的情况下,只允许访问属于孔隙空间骨架的体元。沿着孔隙空间骨架的两条这样的最短路径(从左到右)如图2h中红色部分所示。最后,我们考虑这些最短路径的长度除以起始和目标平面之间的欧氏距离的分布。该分布的均值和标准差分别用和表示。在本文中考虑的所有方向相关的微观结构特征的情况下,这些量分别为三个笛卡尔轴方向中的每一个计算,然后平均。
请注意,存在各种计算三维二值图像骨架的方法,这反过来会影响几何扭曲度的计算Soille (2013);萨哈等人(2016)。
我们现在提出的统计方法将在第3节中用于对壤土和砂土样品进行全面的结构分析,以及建立微观结构-性质关系,定量表征三维孔隙空间形态和土壤气体扩散的几何描述符之间的联系。特别是,在3.2节中,考虑了基于不同的三维孔隙空间形态描述符集的m因子预测的回归公式。一般来说,与数据科学中的其他方法(如神经网络)相比,这种方法产生的结果更容易解释。
3.2节中考虑的回归公式包含少量回归参数,这些回归参数通过训练数据进行拟合,即选择2.2节中描述的4608个子样本中的一小部分来确定回归参数的“最优”值。为了计算这些参数,使用了python包scipy Virtanen et al.(2020)中实现的Levenberg-Marquardt算法mor
为了评估回归公式的性能,我们选择了尚未用于模型拟合的子样本作为测试数据。然后,通过计算决定系数(记为)和平均绝对百分比误差(记为)来量化拟合优度。这两个量定义为
(4)其中,表示2.3节(基本真值)中通过数值模拟计算得到的m -因子,为的平均值,表示由经验推导的回归公式得到的m -因子。
为了拟合模型参数,我们使用了来自壤土和砂土的所有子样本和深度的数据(3072个子样本)。模型验证的手段和从壤土和砂(1536子样本)的深度进行的子样本。本研究中考虑的所有回归公式的参数都是在相同的(训练)数据集上进行拟合的,而拟合回归公式的验证是在未用于拟合的深度的子样本上进行的。通过对不同类型的土壤(壤土和砂土)进行模型拟合和验证,我们可以证明最佳拟合回归公式是适用于一般土壤微观结构,还是只适用于与模型拟合的结构非常相似的结构。
2.4节中所述的几何描述符用于定量表征本文所考虑的土壤亚样的三维微观结构。图3显示了分别从壤土和砂土中获得的子样本的各种几何描述符的直方图。结果表明,在选择的尺度下,孔隙度和收缩度等描述符在相同土壤质地的子样本之间变化很大,而在壤土和沙子之间平均差异很小,见图3a和f。因此,这些描述符可能对区分两种土壤质地的纹理不太有用,但对于描述来自给定土壤质地的单个样品的变化非常有用。另一方面,像比表面积S和平均弦长这样的描述符对于两种土壤纹理的表现相当不同,见图3b和c。因此,它们似乎比和更好地捕捉了纹理之间的形态差异。
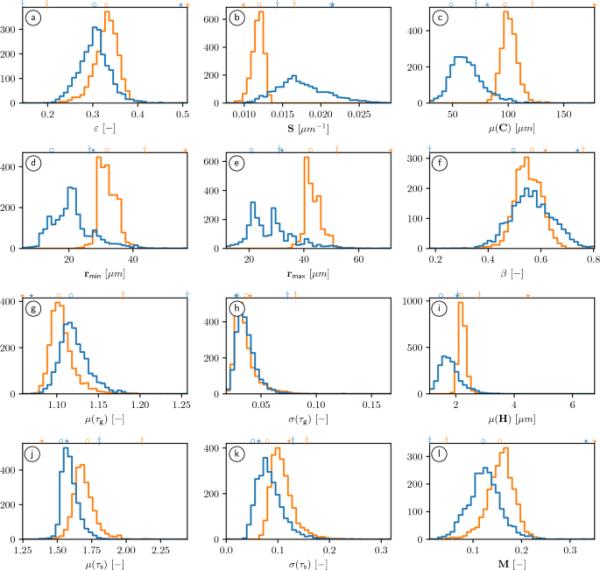
几何描述因子直方图,即孔隙度(a)、比表面积(b)、平均弦长(c)、瓶颈半径(d)、特征孔隙半径(e)、收缩性(f)、测地线扭曲度的平均值和标准差(g, h)、到固相的平均距离(i)、几何扭曲度的平均值和标准差(j),以及分别从壤土(蓝色)和砂(橙色)子样本的层析成像数据计算出的m因子(l)。符号,和表示图1所示子样本的值
通过考虑描述符对的二元概率密度,可以获得更详细的土壤质地表征,见图4。虽然获得的壤土和砂子样本的平均弦长单变量直方图显示出一定的重叠(见图3c),但联合(双变量)概率密度和平均球面接触距离可以可靠地区分壤土和砂,见图4b。
在查看图3g和图j(也参见图4e)时,我们观察到(测地线和几何)扭曲的两个概念的结果是相当不同的。特别是砂土的平均测地线扭曲度小于壤土的相应值(即砂土的孔隙空间路径比壤土短),而砂土的平均几何扭曲度更大。这可能是由于砂比壤土包含更大的孔隙,使得沿粗骨架的路径变得相对较长,而壤土中观察到的更细的孔隙结构导致具有大量节点的骨架,更接近孔隙空间的实际轴线。(测地线和几何)扭曲的两个概念将在第4节中进一步讨论它们作为微观结构-性质关系的几何描述符的用途。
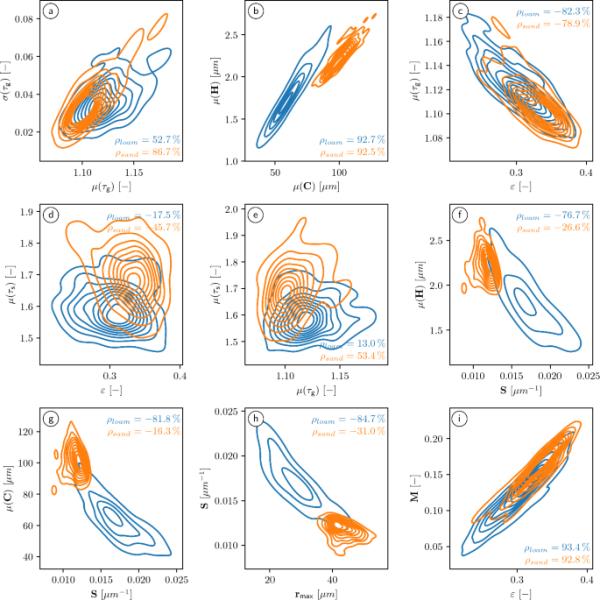
几何描述符对的二元概率密度,可视化为基于核密度估计的等高线图,已获得壤土(蓝色)或沙子(橙色)的立方子样本。此外,给出了每个描述符对的Pearson相关系数值,分别计算了壤土和砂土
本文所考虑的所有几何描述符对之间的相关系数的完整分析在附录中提供,见图7。对于选定的几何描述符对,图4显示了通过核密度估计获得的二元概率密度以及相应的Pearson相关系数。除了,图4中所示的所有其他几何描述符对的接缝密度强烈依赖于所考虑的土壤质地,这再次突出了壤土和沙子之间的结构差异。这表明,任何用这对几何描述符之一来表示m因子的回归公式都需要特别适应沙子和壤土的不同质地。反之亦然,基于和的回归公式可能独立于所考虑的土壤质地而有效。
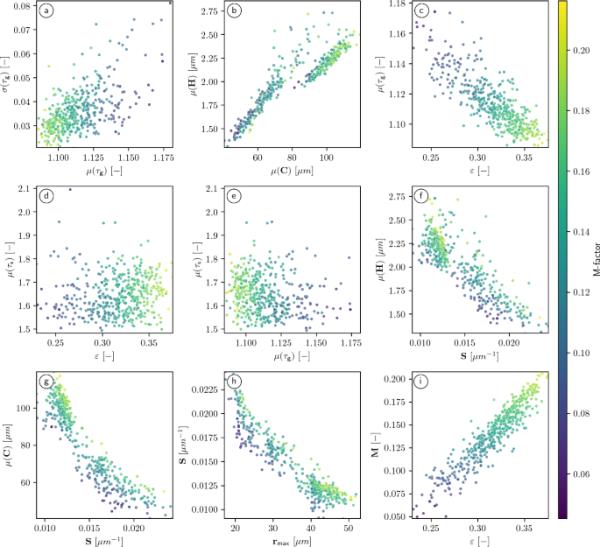
散点图显示了m因子对各种几何描述符的依赖性。数据点的颜色(较亮或较暗)表示相应m因子的值是高还是低。在这个图中,我们不区分这两种土壤质地。为了表述清晰,我们只使用随机选择的4608个立方子样本来生成每个子图中的461个数点
图5所示的散点图说明了m因子对各种几何描述符对的依赖性。在本节中,我们将考虑几个经验推导的回归公式,这些公式将用于量化微观结构-性质关系,特别是用于根据适当选择的三维孔隙空间形态几何描述符向量的知识预测m因子。
给出了一个只考虑孔隙率的简单回归公式
(5)这种幂律类型的回归公式在文献中经常使用,其中最著名的例子可能是Buckingham公式()Buckingham (1904), Millington - Quirk公式()Millington and Quirk公式(1961),Marshall () Marshall(1959)导出的公式,以及Lai等人的工作。赖等人(1976)。本文考虑的数据导致,它正好在Buckingham和Millington-Quirk公式中使用的值之间,但最接近Lai等人的值。赖等人(1976)。
另一个简单的回归公式由
(6)例如,在Currie (1960) (), Currie(1961)()和Grable和Siemer(1968)()中使用了该方法。此外,公式
(7)在Richter和Gro?gebauer(1978)中引入了和,下面考虑。此外,还有许多其他仅涉及孔隙度的预测公式,如Holzer et al. (2022);详情请参阅Shen and Chen(2007)。然而,对这类公式的进一步考虑超出了本文的范围,本文现在特别关注经验推导的回归公式,这些公式除了孔隙度之外,还涉及三维孔隙空间形态的进一步(更复杂)描述符,如平均测地扭曲度或收缩度。特别地,我们考虑这个公式
(8)该技术最初由Stenzel等人(2016)(with)引入,并在Prifling等人(2021)(with)中改装为63,000个虚拟生成的微观结构。
由于式(8)在稀释极限(即为)下不成立,修正后的公式
(9)已在Neumann等人(2020)(with)和Prifling等人(2021)(with)中使用,其中收缩性现在出现在孔隙度指数中。
除了基于孔隙度、收缩度和平均测地线扭曲度的公式外,还可以考虑三维孔隙空间形态的进一步几何描述符。例如,公式
(10)Barman等人(2019)在(with)中引入了该方法,Prifling等人(2021)(with)也考虑了该方法,该方法使用(测地线或几何)扭曲度的标准偏差作为额外的几何描述符。
此外,我们考虑公式
(11)这在文献中还没有被考虑过。一般来说,文献中很少使用比表面积S来预测扩散特性。然而,Moldrup等人(2001)提出了这种回归公式的一个特殊情况,该公式使用了该公式。然而,这种回归公式会导致m因子为负值。相反,式(11)保证。
最后,利用的方法预测m因子
(12)其中除孔隙率外,还包含孔隙空间内随机选取的点与固相的平均弦长和平均球面接触距离之比。后一个量可以看作是某种形状信息,因为在式(12)中,对于越拉长的孔隙,这个商越大。
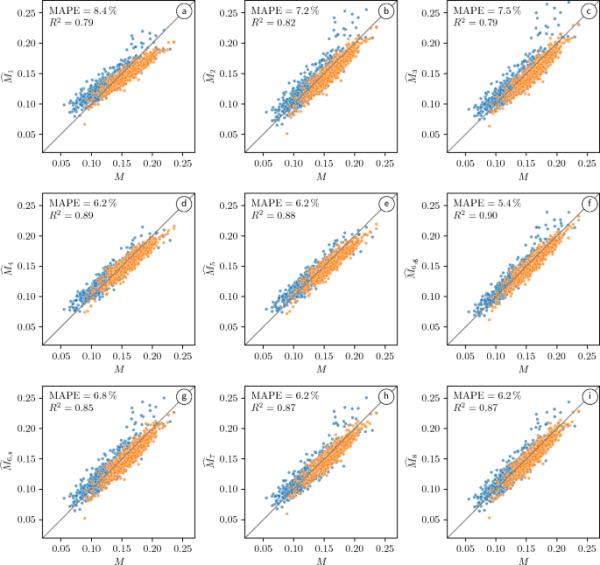
通过数值模拟获得的m因子值与壤土(蓝色)或砂(橙色)测试数据获得的预测m因子值的散点图可视化。在式中给出的预测公式中出现的参数(5) ~(12)拟合到壤土和砂土的整个训练数据中,见表1。特别是,Eq.(10),即,出现了两次,因为同时考虑了测地线和几何扭曲的概念
首先,我们考虑这样一种情况,即从壤土和沙子样本中获得的数据(在深度为5和)用于训练。通过数值模拟得到的m因子值与壤土或砂土试验数据预测得到的m因子值的散点图如图6所示,其中的参数出现在方程给出的预测公式中。(5) -(12)拟合到壤土和砂土的整个训练数据中,见表1。决定系数()和平均绝对百分比误差()的结果值也见图6。此外,我们比较了由方程给出的回归公式的性能。(5) ~(12),其中模型参数与本文考虑的数据拟合,采用文献中先前提出的回归公式拟合,见表2。请记住,当使用后一种公式时,我们没有重新调整模型参数,而是使用原始论文中基于不同类型的数据和使用不同的方法方法得出的相同参数值。
正如所料,由于公式(5)的简单性,它在3.2节中所有的预测公式中表现最差。在这种情况下,由于只使用孔隙度来表征孔隙空间的形态,因此忽略了三维孔隙空间形态的重要结构细节。对于式(5),将其拟合到本文考虑的整个训练数据集,得到。该值大致在1.5 Marshall(1959)和2 Buckingham(1904)之间,但与Millington and Quirk(1961)和Lai et al.(1976)得出的值相当接近。当引入额外的模型参数时,如式。(6)、(7),可分别化简为、。然而,将方程(6)拟合到我们的土壤数据中,得到的值与Grable和Siemer(1968)中得到的值大不相同。由于本研究和Currie(1961)得出的孔隙度指数值存在较大差异;Grable和Siemer(1968),从我们的土壤数据中得出的和的方程(6)的预测能力明显更好,这并不奇怪。另一方面,请注意,我们在式(6)中得到的值与Currie(1960)中得到的值相似。在Currie(1961)中得出的结果中,将已有的回归公式直接应用于当前的土壤数据表现得相当好(导致a),尽管将回归参数重新调整到本文中考虑的土壤数据中(如预期的那样)会得到更好的结果。对于式(7),有趣的是,尽管和的参数值与本文推导的非常接近,但与Richter和Gro?gebauer(1978)的预测能力相比,选择和得到的预测能力明显更好。
通过在回归公式中加入更多三维孔隙空间形态的几何描述符,可以显著提高预测能力。然而,将式(8)中的模型参数拟合到我们的土壤数据会导致,即收缩性在m因子的预测中仅起可忽略不计的作用。Prifling等人(2021)已经观察到这种效应,其中63,000个微观结构被用于模型拟合。此外,将Prifling et al.(2021)和Stenzel et al.(2016)导出的回归公式直接应用于现有土壤数据,可以获得表2中列出的所有(先前导出的)公式中最好的结果。一般来说,与式中给出的预测公式相比,使用式(8)可以显著提高验证分数和。(5)?(7),仅使用孔隙率。这强调了平均测地线扭曲对多孔介质中弥漫性质量输运预测的影响。有趣的是,我们在式(9)中得到的收缩系数不等于零,见表1。这与Prifling et al.(2021)和Neumann et al.(2020)得出的结果相符。无论如何,我们发现(9)式给出的回归公式的预测能力与(8)式相似,尽管(8)式的指数我们得到的值接近于零,即实际上(8)式根本不包括收缩性。
注意,使用式(10)预测m因子时,预测能力可以进一步提高,其中式(10)给出的回归公式是基于孔隙度、测地线平均扭曲度和测地线扭曲度的标准差。在这种情况下,对于验证分数和,我们得到和,这是本文考虑的所有预测公式中最好的结果。这表明,不仅最短路径长度的平均值对弥漫性质量输运的预测有意义,而且对相应的标准差也有意义。但是,将式(10)与Prifling et al.(2021)和Barman et al.(2019)中推导的回归参数值直接应用,分别得到和。这种巨大的差异可以用回归参数的对应值来解释,特别是Prifling等人(2021)()和Barman等人(2019)()的结果与我们在本文中得到的结果()之间的指数值存在显著差异。
我们还注意到,公式(11)使用孔隙率、比表面积和特征孔隙半径,得到的结果与公式(11)相似。(8)和(9)。有趣的是,使用预测m因子被证明是有用的,即使方程(8)拟合我们的土壤数据实际上没有利用收缩性,这是密切相关的。最后,m因子可以通过式(12)进行预测。这将导致和,它们与从eq中获得的值相似。(8)、(9)、(11)见表1。因此,式(11)中由平均弦长与平均球面接触距离之比给出的无因次量(表征孔隙形状)与孔隙度相结合,非常适合预测扩散特性。
值得一提的是,一般来说,关于m因子预测的最佳几何描述符的问题很难回答,因为某些似乎与弥漫性质量输运无关的几何描述符,当它们与进一步的微观结构特征相结合时,可以很好地适用于建立微观结构-性能关系。此外,对于三维微结构的某些特征,文献中对同一结构特征考虑了几种不同的几何描述符。例如,正如在2.4节中已经提到的,存在不同的扭曲度概念,在预测土壤弥漫性质量输运方面,测地线扭曲度优于几何扭曲度,见表1中和的验证分数。这可能是由于定义中考虑的孔隙空间骨架只部分考虑了孔隙空间的复杂形态。另一方面,毫不奇怪,所有用于预测m因子的回归公式,其参数已拟合到本文所考虑的土壤数据中,在验证分数和之前在文献中导出的相应回归公式(并拟合到其他类型的图像数据)方面都表现得更好,见表1和表2。这突出了使用适当选择的数据集的重要性,这些数据集代表了所考虑的3D微观结构的性质,用于拟合第3.2节中所述回归公式的参数。
回想一下,到目前为止,我们考虑的情况是,从壤土和沙子样本中获得的数据(在深度为5和)用于训练。关于微观结构-属性关系的结果,其中只有一部分训练数据(无论是壤土还是沙子)用于拟合回归参数,可以在附录中找到,见图8、9和10。正如预期的那样,在大多数情况下,与使用完整的训练数据相比,仅使用训练数据的一个子集进行拟合时,预测能力会降低。然而,仅使用砂体数据进行拟合和验证通常会获得更好的结果。这可能是由于许多描述符以及m因子显示砂比壤土的变化更小。此外,与之前考虑的情况类似,测地线扭曲度的概念在预测扩散输运性质方面比几何扭曲度的结果更好。此外,可以看出,式(10)似乎具有相当的鲁棒性,即使基于一种土壤质地拟合相应的回归参数并应用于另一种土壤质地,该回归公式的预测能力也很大。但是,请注意,如果将本节讨论的回归公式应用于其他类型的三维微结构,则可能仅在有限程度上有效,这些类型与本文考虑的土壤样品有很大不同。
此外,本研究中的微观结构-性能关系是在相当小的体积上建立的()。这有一个有利的影响,即m因子在所有子样品中的变异性对于填充土壤来说是相当大的,因此适合于测试不同模型的准确性。然而,不仅是扩散,还有一些三维孔隙空间形态的几何描述符,如扭曲度,都是尺度相关的ghanbararian(2022)。因此,将在即将到来的研究中测试这些模型在多大程度上适用于更大的土壤体积。
本文研究了壤土和砂土两种不同质地土壤的三维孔隙形态几何描述符与扩散输运特性之间的关系。为此,利用x射线计算机断层扫描技术对5、10和深度的砂和壤土样品进行了成像,并将其分割为两相(孔隙和固体)。用这种方法得到的6幅二值三维图像,分别被分割成768个互不重叠的子样本,共得到4608个子样本。对于这些子样本中的每一个,孔隙空间的三维形态都通过各种几何描述子来表征,其中包括孔隙率以及比表面积、平均测地线扭曲度、收缩度和孔隙空间的平均球面接触距离。除了孔隙空间的几何表征外,还通过数值求解非均匀通量边界条件下的拉普拉斯方程计算了扩散输运性质。
对三维孔隙空间形态进行了全面的统计分析,通过确定单个几何描述符和成对几何描述符的单变量和双变量概率分布,量化砂和壤土之间的结构差异。其中,孔隙空间的比表面积和平均弦长可以用来区分壤土和砂土。
此外,利用参数回归公式研究了壤土和砂土的微观结构-性质关系。利用尚未在土壤气体扩散背景下考虑的三维孔隙空间形态的复杂几何描述符,可以显著提高回归公式的预测能力。其中,考虑的三维微观结构描述符包括测地线扭曲度、收缩度和平均弦长的平均值和标准差。特别是,研究表明,在预测扩散特性方面,测地线扭曲度的概念优于基于孔隙空间骨架化的几何扭曲度。此外,通过将回归参数拟合到一种土壤质地,并将得到的回归公式应用到另一种土壤质地,研究了回归公式的稳健性。结果表明,最理想的回归公式是基于孔隙度以及测地线扭曲度的均值和标准差,平均绝对百分比误差约为5%。一般来说,参数回归公式的预测能力取决于所考虑的具体土壤质地,最佳回归公式在拟合一种土壤质地并应用于另一种土壤质地的情况下也表现良好。
总之,通过我们的分析,我们对三维土壤微观结构的某些结构特征的相关性有了更好的理解,我们通过几何描述符测量了扩散传输特性,与文献中传统回归公式的精度相比,我们能够更准确地预测它们。未来研究的一个可能的主题是将这种分析扩展到不同长度尺度的结构。发展一种适当的多尺度方法将允许预测非常大的土壤结构的扩散特性。此外,目前的方法可以应用于更实际的发展土壤,其中明显的各向异性效应是预期的。
发表评论
暂时没有评论,来抢沙发吧~